Page 18 - Construction d’une géométrie en Relativité [ebook] v5-1

Les coordonnées du point courant P de l’espace
dans R’’c sont :

x’’ = x - vt
y’’ = y
z’’ = z
x’’ = -( x - vt ) tg(θ)
y’’ = 0
z’’ = 0

Retour sur le domaine de définition de l’angle θ
( 0 ≤ θ < ) :

Le changement de variable était le suivant :
nous posions sin² (θ) = .
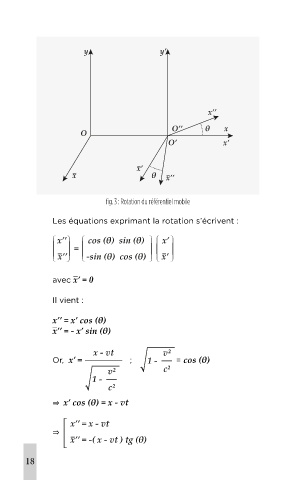
fig. 3 : Rotation du référentiel mobile

Les équations exprimant la rotation s’écrivent :
Il vient : sin (θ) = avec sin (θ) ≥ 0 .

L’angle θ étant défini à 2kπ près, nous nous limitons
aux valeurs de θ comprises entre 0 et 2π ;
avec x’ = 0
sin(θ)≥0 impose donc 0 ≤ θ ≤ π .
Il vient :

x’’ = x’ cos (θ) La valeur θ = est interdite car v < c .
x’’ = - x’ sin (θ)

Le domaine de définition envisageable de θ est donc
Or, x’ = ; = cos (θ)
[ 0 , ] et/ou [ , π ] .

⇒ x’ cos (θ) = x - vt Compte tenu de la nécessité d’une bijection entre θ
et v, le domaine de définition de θ appartiendra soit au
premier soit au deuxième des domaines ci-dessus.
⇒

18 19