Page 34 - Construction d’une géométrie en Relativité [ebook] v5-1
P. 34
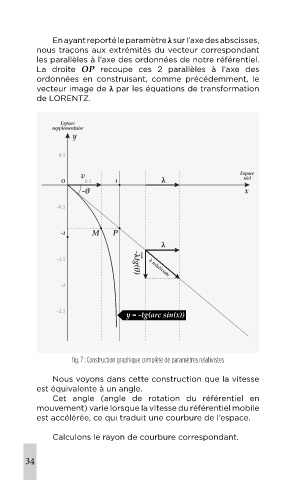
En ayant reporté le paramètre λ sur l’axe des abscisses, Courbure de l’espace dans des
nous traçons aux extrémités du vecteur correspondant référentiels en accélération axiale
les parallèles à l’axe des ordonnées de notre référentiel.
La droite OP recoupe ces 2 parallèles à l’axe des
ordonnées en construisant, comme précédemment, le Dans le référentiel fixe, le référentiel mobile possède
vecteur image de λ par les équations de transformation un mouvement de translation accélérée le long de l’axe
de LORENTZ. des abscisses du référentiel fixe.
A l’instant t, l’origine du référentiel mobile se trouve
au point O. Soit M un point quelconque de l’axe de
translation du référentiel mobile (axe des abscisses du
référentiel fixe). M’ représente ce point dans le référentiel
mobile après rotation.
L’origine du référentiel mobile est animée à cet
instant de la vitesse v et parcourt la distance dx = v.dt
durant un intervalle de temps infinitésimal dt.
D’après ce qui précède, l’image ds de cet élément dx
dans le référentiel mobile est représentée (voir figure 7)
par un vecteur de coordonnées :
Cet élément différentiel ds au point M’ est porté par
la droite OP de pente –tg(θ) (conformément à la figure
7).
Pendant l’intervalle de temps dt la pente p de
l’élément différentiel ds varie de :
fig. 7 : Construction graphique complète de paramètres relativistes ;
Nous voyons dans cette construction que la vitesse
est équivalente à un angle. Nous supposons que la vitesse v a une valeur positive
Cet angle (angle de rotation du référentiel en ce qui est toujours possible avec un changement d’axes.
mouvement) varie lorsque la vitesse du référentiel mobile
est accélérée, ce qui traduit une courbure de l’espace.
Calculons le rayon de courbure correspondant.
34 35